Answer:
a) 0.1667 = 16.67% probability that the student requires more than 55 minutes to complete the quiz.
b) 0.3333 = 33.33% probability that the student completes the quiz in a time between 30 and 40 minutes.
c) 0% probability that the student completes the quiz in exactly 37.23 minutes.
Explanation:
Uniform probability distribution:
An uniform distribution has two bounds, a and b.
The probability of finding a value of at lower than x is:

The probability of finding a value between c and d is:
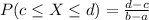
The probability of finding a value above x is:
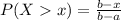
Uniformly distributed between 30 and 60 minutes.
This means that
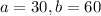
a. The student requires more than 55 minutes to complete the quiz.

0.1667 = 16.67% probability that the student requires more than 55 minutes to complete the quiz.
b. The student completes the quiz in a time between 30 and 40 minutes.
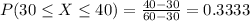
0.3333 = 33.33% probability that the student completes the quiz in a time between 30 and 40 minutes.
c. The student completes the quiz in exactly 37.23 minutes.
Probability of an exact value in a continuous distribution, such as the uniform distribution, is 0%, so:
0% probability that the student completes the quiz in exactly 37.23 minutes.