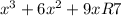Answer:
Explanation:
If we have 5 terms to the right of the -1 outside the box thing, that means that our original polynomial is a 4th degree (the degree is one lower than the number of terms in order to allow for the constant which has no variable). Set up the synthetic division as shown in the problem. The rule is to bring down the first term, the 1 to the right of the box, multiply it by the number outside, -1, and put that product up under the next number in line inside the box. Like this:
-1 | 1 7 15 9 7
-1
1
Now add straight down, multiply the sum by -1 and put that product up under the next term in line, the 15:
-1 | 1 7 15 9 7
-1 -6
1 6
Then add straight down again, multiply the sum by -1 and put that product up under the next term in line, the 9:
-1 | 1 7 15 9 7
-1 -6 -9
1 6 9
Then do the same thing. Add straight down, multiply the sum by -1 and put the product up under the next term in line, the 7:
-1 | 1 7 15 9 7
-1 -6 -9 0
1 6 9 0 7
This is the final result. The last number, the 7 is the remainder, but the rest of it makes up what we call the depressed polynomial and is a polynomial that is one degree less than the degree we started with. So this depressed polynomial is a 3rd degree. The numbers are the coefficients on the x terms:
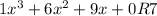or more simply stated:
