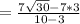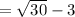Answer:

Explanation:
Write the given expression in a numerical format:

A logical first step to take in this problem is to convert the denominator to a rational value. Currently, the denominator is an irrational value, meaning that it is a never-ending value. One wants it to be a rational value. This can be done by multiplying the denominator by its conjugate. The conjugate of this number is simply the denominator with the second addend times negative one. Remember to multiply both the numerator and denominator by this value, as a number over itself is the same as multiply by (1) Use this idea here:

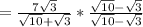
Simplify,
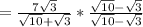
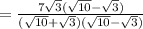

Note that any value times itself under the radical is equal to the number, meaning (
 ). Apply this to the problem,
). Apply this to the problem,