Question

The number of cities in a region over time is represented by the function C(x)=2.9(1.05)^x. The approximate number of people per city is represented but the function P(x)=(1.05)^3x+5

Which Function best describes T(x), the approximate population in the region?

HELP!!! PLS

Answer 1

B.
`T(x) = 2.9\cdot (1.05)^(4\cdot x + 5)`

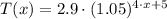
Explanation:

The approximate population in the region is the product of the number of cities in a region and the approximate number of people per city, that is:

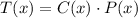`T(x) = C(x)\cdot P(x)` (1)

If we know that
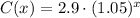`C(x) = 2.9\cdot (1.05)^(x)` and
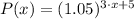`P(x) = (1.05)^(3\cdot x + 5)`, then the formula for the approximate population in the region is:

`T(x) = [2.9\cdot (1.05)^(x)]\cdot [(1.05)^(3\cdot x + 5)]`

`T(x) = 2.9\cdot (1.05)^(4\cdot x + 5)`

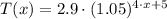
Hence, correct answer is B.