Answer:
Approximately
 . (Assuming that this table is level, and that the gravitational field strength is
. (Assuming that this table is level, and that the gravitational field strength is
 .
.
Step-by-step explanation:
Convert the dimensions of this book to standard units:
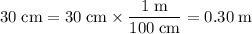 .
.
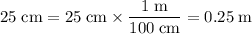 .
.
Calculate the surface area of this book:
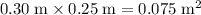 .
.
Pressure is the ratio between normal force and the area over which this force is applied.
 .
.
Equivalently:
 .
.
In this question,
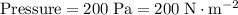 .
.
It was found that
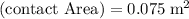 (assuming that the entire side of this book is in contact with the table.
(assuming that the entire side of this book is in contact with the table.
Hence:
 .
.
If that the table is level, this normal force would be equal to the weight of this book:
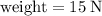 .
.
Assuming that the gravitational field strength is
 . The mass of this book would be:
. The mass of this book would be:
 .
.