Question

1) Consider an electric power transmission line that carries a constant electric current of i = 500 A. The cylindrical copper cable used to transmit this current has a diameter o = 2.00 cm and a length L = 150 km. If there are 8.43x10^28 free electrons per cubic meter (m^3 ) in the cable, calculate how long it would take for an electron to cross the entire length of the transmitter line.

R= 10 x 10^6 years

Answer 1

t = 1.27 x 10⁹ s

Step-by-step explanation:

First, we will find the volume of the wire:

`Volume = V = (A)(L)`

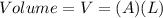
where,

A = Cross-sectional area of wire = πr² = π(1 cm)² = π(0.01 m)² = 3.14 x 10⁻⁴ m²

L = Length of wire = 150 km = 150000 m

Therefore,

`V = (3.14\ x\ 10^(-4)\ m^2)(150000\ m)`

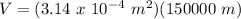
V = 47.12 m³

Now, we will find the number of electrons in the wire:

No. of electrons = n = (Electrons per unit Volume)(V)

n = (8.43 x 10²⁸ electrons/m³)(47.12 m³)

n = 3.97 x 10³⁰ electrons

Now, we will use the formula of current to find out the time taken by each electron to cross the wire:

`I = (q)/(t)`

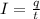
where,

t = time = ?

I = current = 500 A

q = total charge = (n)(chareg on one electron)

q = (3.97 x 10³⁰ electrons)(1.6 x 10⁻¹⁹ C/electron)

q = 6.36 x 10¹¹ C

Therefore,

`500\ A = (6.36\ x\ 10^(11)\ C)/(t)\\\\t = (6.36\ x\ 10^(11)\ C)/(500\ A)`

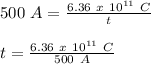
t = 1.27 x 10⁹ s