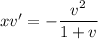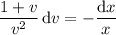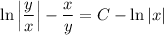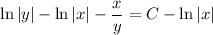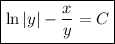Question

Answer theas question

Answer 1

(1) Both equations in (a) and (b) are separable.

(a)

`\frac xy y' = (2y^2+1)/(x+1) \implies (\mathrm dy)/(y(2y^2+1)) = (\mathrm dx)/(x(x+1))`

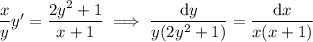
Expand both sides into partial fractions.

`\left(\frac1y - (2y)/(2y^2+1)\right)\,\mathrm dy = \left(\frac1x - \frac1{x+1}\right)\,\mathrm dx`

Integrate both sides:

`\ln|y| - \frac12 \ln\left(2y^2+1\right) = \ln|x| - \ln|x+1| + C`

`\ln\left|\frac y{√(2y^2+1)}\right| = \ln\left|\frac x{x+1}\right| + C`

`\frac y{√(2y^2+1)} = (Cx)/(x+1)`

`\boxed{(y^2)/(2y^2+1) = (Cx^2)/((x+1)^2)}`

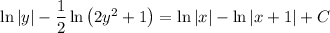
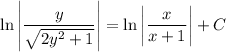
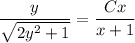
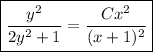
(You could solve for y explicitly, but that's just more work.)

(b)

`e^(x+y)y' = 3x \implies e^y\,\mathrm dy = 3xe^(-x)\,\mathrm dx`

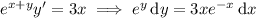
Integrate both sides:

`e^y = -3e^(-x)(x+1) + C`

`\ln(e^y) = \ln\left(C - 3e^(-x)(x+1)\right)`

`\boxed{y = \ln\left(C - 3e^(-x)(x+1)\right)}`

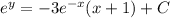
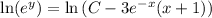
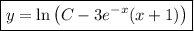
(2)

(a)

`y' + \sec(x)y = \cos(x)`

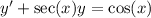
Multiply both sides by an integrating factor, sec(x) + tan(x) :

`(\sec(x)+\tan(x))y' + \sec(x) (\sec(x) + \tan(x)) y = \cos(x) (\sec(x) + \tan(x))`

`(\sec(x)+\tan(x))y' + (\sec^2(x) + \sec(x)\tan(x)) y = 1 + \sin(x)`

`\bigg((\sec(x)+\tan(x))y\bigg)' = 1 + \sin(x)`

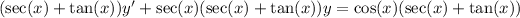
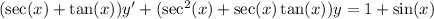
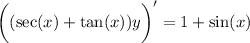
Integrate both sides and solve for y :

`(\sec(x)+\tan(x))y = x - \cos(x) + C`

`y=(x-\cos(x) + C)/(\sec(x) + \tan(x))`

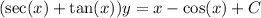
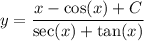
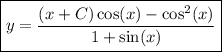
`\boxed{y=((x+C)\cos(x) - \cos^2(x))/(1+\sin(x))}`

(b)

`y' + y = \frac{e^x-e^(-x)}2`

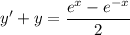
(Note that the right side is also written as sinh(x).)

Multiply both sides by e ˣ :

`e^x y' + e^x y = \frac{e^(2x)-1}2`

`\left(e^xy\right)' = \frac{e^(2x)-1}2`

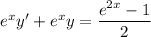
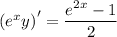
Integrate both sides and solve for y :

`e^xy = \frac{e^(2x)-2x}4 + C`

`\boxed{y=\frac{e^x-2xe^(-x)}4 + Ce^(-x)}`

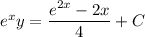
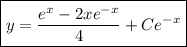
(c) I've covered this in an earlier question of yours.

(d)

`y'=\frac y{x+y}`

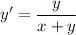
Multiply through the right side by x/x :

`y' = (\frac yx)/(1+\frac yx)`

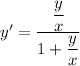
Substitute y(x) = x v(x), so that y' = xv' + v, and the DE becomes separable:

`xv' + v = (v)/(1+v)`

`xv' = -(v^2)/(1+v)`

`(1+v)/(v^2)\,\mathrm dv = -\frac{\mathrm dx}x`

`-\frac1v + \ln|v| = -\ln|x| + C`

`\ln\left|\frac yx\right| -\frac xy = C - \ln|x|`

`\ln|y| - \ln|x|  -\frac xy = C - \ln|x|`

`\boxed -\frac xy = C`