Question

Consider the complex number on the complex plane and the complex number z2 = 6 – 3i.

When z1 and z2 are added together, the result moves z1 6 units
and 3 units
.

The real part of z1 + z2 is
.

The imaginary part of z1 + z2 is
i.

Answer 1

See below

Explanation:

So, on the complex plane, we see that
`z_1=2+1i`

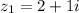
Therefore,
`z_1+z_2=(2+1i)+(6-3i)=8-2i`

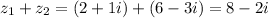
Since we added the complex numbers, we can see that the real part of
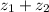`z_1+z_2` is 8 and the imaginary part of
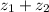`z_1+z_2` is -2. Remember that complex numbers are written in the form of
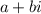`a+bi`, so either the real or imaginary part can both be negative.

Answer 2

beep

Explanation:

edge 2022

good luck :)