Question

Find the distance between the points (2, 4) and (8, -8) on a coordinate plane, to the nearest whole number.

A.7
B.11
C.13
D.16

Answer 1

C

Explanation:

distance between two points formula:

`d = \sqrt{( x2 - x1) ^(2) + (y2 - y1) ^(2) }`

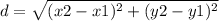
where the x and y values are derived from the known points

we are given the points (2, 4) and (8, -8)

given these two points let's define each variable

x1 = 2

x2 = 8

y1 = 4

y2 = -8

we now substitute in these values into the formula

`d = \sqrt{(8 - 2) ^(2) + ( - 8 - 4)^(2) }`

now we evaluate the expression using PEMDAS

first we do the subtraction inside of the parenthesis

8 - 2 = 6

-8 - 4 = -12

d = sqrt(6)^2 + (-12)^2

next we do the exponents

6^2 = 36

-12^2 = 144

d = sqrt( 144 + 36 )

next do the addition inside of the parenthesis

144 + 36 = 180

d = sqrt ( 180 )

finally we do the square root of 180

sqrt ( 180 ) = 13 ( rounded to the nearest whole )

d = 13