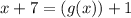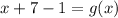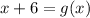Answer:
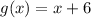
Explanation:
The problem gives one the following information:
![h(x)=(f\ \ o\ \ g)(x)\\\\h(x)=\sqrt[4]{x+7}\\f(x)=\sqrt[4]{x+1}](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/sensvgzzo7jxap1x8hfa5e.png)
This problem now requires one to find the function (
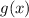 ).
).
The format:
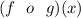
Is another way of writing a composition of a function. In essence, it indicates this operation:
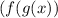
This means that one has to input one function into another. In other words, substitute one function into another in place of the variable, then simplify and solve to find the new function that is derived from this operation. Since it is given that (
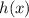 ) is the function resulting from the composition of (
) is the function resulting from the composition of (
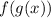 ), an equation can be formed. Treat the evaluator (
), an equation can be formed. Treat the evaluator (
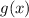 ) as another variable. Then simplify and solve the equation to find the function that represents (
) as another variable. Then simplify and solve the equation to find the function that represents (
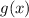 ).
).
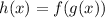
Substitute,
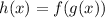
![\sqrt[4]{x+7}=\sqrt[4]{(g(x)+1}](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/kw2kndpau3vsp9fkuzppki.png)
Since both numbers are equivalent to each other when one takes the quartic root of the numbers, the numbers underneath the radical must be equivalent to each other. Therefore, one can state the following:
![\sqrt[4]{x+7}=\sqrt[4]{(g(x)+1}](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/kw2kndpau3vsp9fkuzppki.png)
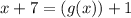
Inverse operations: