Given:
The inequality is:
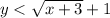
To find:
The domain and range of the given inequality.
Solution:
We have,
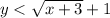
The related equation is:
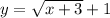
This equation is defined if:
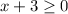
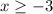
In the given inequality, the sign of inequality is <, it means the points on the boundary line are not included in the solution set. Thus, -3 is not included in the domain.
So, the domain of the given inequality is x>-3.
We know that,
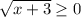
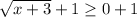
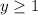
The points on the boundary line are not included in the solution set. Thus, 1 is not included in the range.
So, the domain of the given inequality is y>1.
Therefore, the correct option is A.