Question

HELP!! Algebra help!! Will give stars thank u so much <333

Answer 1

Answers:

• Part a)
  `\bf{√(x^2+(x^2-3)^2)`
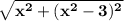
• Part b) 3
• Part c) 2.24
• Part d) 1.58

============================================================

Work Shown:

Part (a)

The origin is the point (0,0) which we'll make the first point, so let (x1,y1) = (0,0)

The other point is of the form (x,y) where y = x^2-3. So the point can be stated as (x2,y2) = (x,y). We'll replace y with x^2-3

We apply the distance formula to say...

`d = √((x_1-x_2)^2+(y_1-y_2)^2)\\\\d = √((0-x)^2+(0-y)^2)\\\\d = √((0-x)^2+(-y)^2)\\\\d = √(x^2 + y^2)\\\\d = √(x^2 + (x^2-3)^2)\\\\`

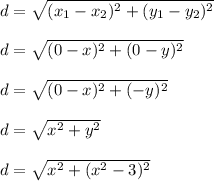
We could expand things out and combine like terms, but that's just extra unneeded work in my opinion.

Saying
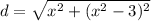`d = √(x^2 + (x^2-3)^2)` is the same as writing d = sqrt(x^2-(x^2-3)^2)

-------------------------------------------

Part (b)

Plug in x = 0 and you should find the following

`d(x) = √(x^2 + (x^2-3)^2)\\\\d(0) = √(0^2 + (0^2-3)^2)\\\\d(0) = √((-3)^2)\\\\d(0) = √(9)\\\\d(0) = 3\\\\`

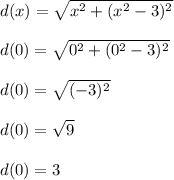
This says that the point (x,y) = (0,3) is 3 units away from the origin (0,0).

-------------------------------------------

Part (c)

Repeat for x = 1

`d(x) = √(x^2 + (x^2-3)^2)\\\\d(1) = √(1^2 + (1^2-3)^2)\\\\d(1) = √(1 + (1-3)^2)\\\\d(1) = √(1 + (-2)^2)\\\\d(1) = √(1 + 4)\\\\d(1) = √(5)\\\\d(1) \approx 2.23606797749979\\\\d(1) \approx 2.24\\\\`

-------------------------------------------

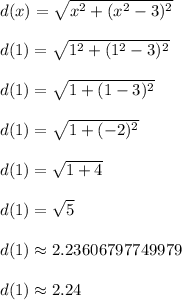
Part (d)

Graph the d(x) function found back in part (a)

Use the minimum function on your graphing calculator to find the lowest point such that x > 0.

See the diagram below. I used GeoGebra to make the graph. Desmos probably has a similar feature (but I'm not entirely sure). If you have a TI83 or TI84, then your calculator has the minimum function feature.

The red point of this diagram is what we're after. That point is approximately (1.58, 1.66)

This means the smallest d can get is d = 1.66 and it happens when x = 1.58 approximately.