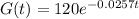Answer:
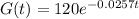
Explanation:
Amount of substance:
The amount of the substance after t minutes is given by:
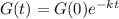
In which G(0) is the initial amount and k is the decay rate.
At the beginning of an experiment, a scientist has 120 grams of radioactive goo.
This means that
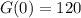 , so:
, so:
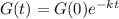
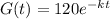
After 135 minutes, her sample has decayed to 3.75 grams.
This means that
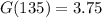 .
.
We use this to find k. So
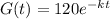
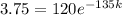
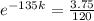
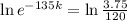
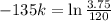
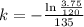
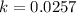
So