Answer:
116 people are expected to have heard the rumor after 6 days total have passed since it was initially spread.
Explanation:
Logistic function:
The logistic function is given by:
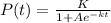
In which:
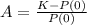
Considering that K is the carrying capacity, k is the growth/decay rate and P(0) is the initial population.
Suppose a rumor is going around a group of 210 people.
This means that
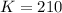
Initially, only 34 members of the group have heard the rumor:
This means that
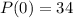 and:
and:
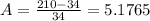
So
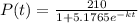
3 days later 69 people have heard it.
This means that
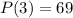 , and we use this to find k.
, and we use this to find k.
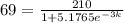
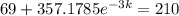
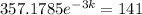
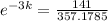
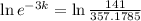
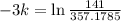
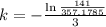
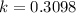
So
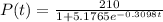
How many people are expected to have heard the rumor after 6 days total have passed since it was initially spread?
This is P(6), so:
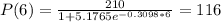
116 people are expected to have heard the rumor after 6 days total have passed since it was initially spread.