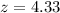Question

Obesity is seen as a growing health problem in many countries, including the United States. To determine whether or not there has been an increase in obesity in men over the past ten years, medical records for 50 randomly sampled men from the year 2000 and for 75 randomly sampled men from the year 2010 were analyzed. Out of the 50 men from 2000, 10 were assigned as obese according to their height and weight while 30 out of the 75 men from 2010 were assigned as obese. Calculate the z-test statistic for this hypothesis test. Round your final answer to 2 decimal places

Answer 1

The z-test statistic for this hypothesis test is
`z = 4.33`

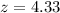
Explanation:

Proportion in 2000:

10 of the 50 men were obese, so:

`p = (10)/(50) = 0.2`

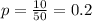
Test if it has increased:

At the null hypothesis, we test if the prevalence of obesity has not increased, that is, the proportion is of 0.2 or less, so:

`H_0: p \leq 0.2`

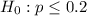
At the alternative hypothesis, we test if this prevalence has increased, that is, the proportion is above 0.2. So

`H_1: p > 0.2`

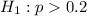
The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

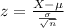
In which X is the sample mean,
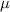`\mu` is the value tested at the null hypothesis,
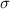`\sigma` is the standard deviation and n is the size of the sample.

0.2 is tested at the null hypothesis:

This means that
`\mu = 0.2, \sigma = √(0.2(1-0.2)) = 0.4`

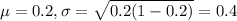
30 out of the 75 men from 2010 were assigned as obese.

This means that
`n = 75, X = (30)/(75) = 0.4`

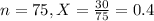
Value of the z-test statistic:

`z = (X - \mu)/((\sigma)/(√(n)))`

`z = (0.4 - 0.2)/((0.4)/(√(75)))`

`z = 4.33`

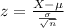
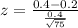
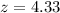
The z-test statistic for this hypothesis test is
`z = 4.33`