Question

Help please i’m so desperate

Answer 1

You're fairly close but not 100% correct.

This function is logarithmic simply because of the presence of "log" in the notation. So you're correct with that statement.

However, we have a vertical asymptote and not a horizontal one. Note how the green function approaches but never touches x = 2. This is a vertical electric fence of sorts. This is due to the fact that log(x) cannot have x = 0. So log(x-2) cannot have x = 2. We can't have x < 2 either.

So you'll need to change that '3' to '2' without quotes of course.

The range is correct. The function can spit out any y value we want. So the range is the set of all real numbers, or we could say -infinity < y < infinity which translates to the interval notation you wrote. The function is increasing because we're going uphill when moving to the right.

The domain is not correct. The domain would be x > 2 to represent the possible x inputs. We can plug in anything larger than 2. The inequality x > 2 translates to the interval notation
`(2, \infty)`

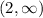
The end behavior portion is half correct. The left side end behavior should be
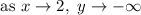`\text{ as } x \to 2, \ y \to -\infty` to represent the idea of getting closer to that electric fence and going off to negative infinity (down the page forever). We don't have x approaching negative infinity because we can't go beyond that fence. The end behavior on the right side is correct.

-------------------

So the answers would be

The function f(x) is a logarithmic function with a vertical asymptote x = 2. The range of the function is
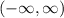`(-\infty, \infty)` and it is increasing on its domain of
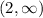`(2, \infty)`. The end behavior on the left side is
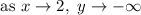`\text{ as } x \to 2, \ y \to -\infty` and the end behavior on the right side is
`\text{ as } x \to \infty, \ y \to \infty`

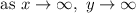
Check out the attached image below.