Question

Question #3 please show steps

Answer 1

A

Explanation:

We are given a table and the function:

`\displaystyle f(x)=\int_(-2)^(x)g(t)\, dt`

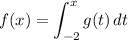
And:

`h(x)=2x+\sin(x)`

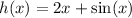
We want to determine the value of x for which h(x) = f'(2).

First, by the Fundamental Theorem of Calculus:

`f'(x)=g(x)`

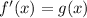
Then by the table:

`f'(2)=g(2)=-2`

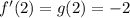
Therefore:

`h(x)=2x+\sin(x)=-2`

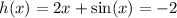
Use graphing technology*:

`x\approx -0.684`

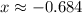
Our answer is A.

*Perhaps there is a way to solve this manually, though I'm not certain.