Given:
The function is:

To find:
The vertical and horizontal asymptotes of the given function.
Solution:
We have,

For vertical asymptotes, equate the denominator and 0.


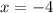
So, the vertical asymptote of the given function is
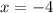 .
.
The degree of the numerator is 1 and the degree of the denominator is also 1.
Since the degrees of numerator and denominator are equal, therefore the horizontal asymptote is:
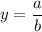
Where, a is the leading coefficient of numerator and b is the leading coefficient of denominator.
Leading coefficient of numerator is 2 and the leading coefficient of denominator is 1, so the horizontal asymptote is:
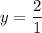
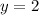
Therefore, the correct option is C.