Question

A quadratic function, f(x) = x2 + bx + 9, is such that there is only one real root. Which of the following are possible values of b?

I. b = 2
II. b = 6
III. b = -6
IV. b = -2

A. I, II, III, and IV
B. I and IV only
C. II and III only
D. I only

Answer 1

C

Explanation:

Remember that we can use the discriminant to determine the amount of roots that a quadratic function has.

If the determinant equals 0, then we only have one real root.

Our function is given by:

`f(x)=x^2+bx+9`

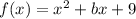
Then the discriminant will be:

`\Delta = b^2-4(1)(9)=b^2-36`

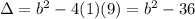
We only have one real root, thus our discriminant must be 0:

`0=b^2-36`

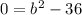
Solve for b:

`b^2=36`

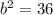
Thus:

`b=\pm 6`

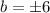
The answer is both II and III.

The final answer, then, is C.