Question

The length of a rectangle is 2 centimeters less than three times its width. Its area is 21 square centimeters. Find the dimensions of the rectangle. Use the​ formula, area=length*width.

Answer 1

The dimensions of the rectangle are 7 by 3 centimeters.

Explanation:

We are given that the length of a rectangle is two centimeters less than three times its width. In other words:

`\displaystyle \ell = 3w-2`

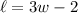
Given that the area of the rectangle is 21 square centimeters, we want to determine the dimensions of the rectangle.

Recall that the area of a rectangle is given by:

`A= w\ell`

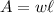
Substitute:

`(21)=w(3w-2)`

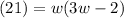
Solve foro the width. Distribute:

`3w^2-2w=21`

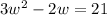
Isolate the equation:

`3w^2-2w-21=0`

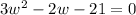
Factor. Find two numbers that multiply to 3(-21) = -63 and add to -2.

-9 and 7 suffice. Hence:

`3w^2-9w+7w-21=0 \\ \\ 3w(w-3)+7(w-3) = 0 \\ \\ (3w+7)(w-3)=0`

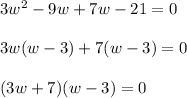
Zero Product Property:

`3w+7=0\text{ or } w-3=0`

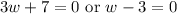
Solve for each case. Hence:

`\displaystyle w = -(7)/(3)\text{ or } w=3`

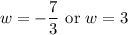
Since width cannot be negative, we can ignore the first solution.

Therefore, our width is three centimeters.

And since the length is two less than three times the width, the length is:

`\ell = 3(3) - 2 = 7`

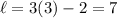
The dimensions of the rectangle are 7 by 3 centimeters.

Answer 2

Area = length x width

Area = 21 square cm

Width = x

Length = 3x + 2

21 = 3x+ 2 * x

21 = 3x ^2 + 2x

Subtract 21 from both sides:

3x^2 + 2x -21 = 0

Use the quadratic formula to solve for x:

-2 +/- sqrt(2^2-4*3(-21))/(2*3)

X = 7/3 and -3

A dimension can’t be a negative value so x needs to be 7/3

Width = x = 7/3 = 2 1/3 cm

Length = 3(7/3) + 2 = 9 cm

Check: 9 x 2 1/3 = 21

Dimensions: width 2 1/3 cm length 9 cm