Question

Given that the average of 2021 different positive integers is 3939, find the minimum possible value of the largest number among those 2021 positive integers.

Answer 1

4049

Explanation:

For a set of N numbers:

{x₁, x₂, ..., xₙ}

The mean is given by:

`M = (x_1 + x_2 + ... + x_n)/(N)`

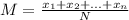
So, if we have 2021 different positive integers, we have N = 2021.

We know that the mean is 3939.

We want to find the minimum possible value of the largest number in the set.

This is kinda trivial but:

We have 2021 numbers = 2020 numbers + 1 number

So we can assume that half of these 2020 numbers are consecutive to and smaller than 3939 and half are larger than and consecutive to 3939, and the remaining number is 3939, then our set is:

{ (3939 - 1010), (3939 + 1009),..., (3939), ..., (3939 + 1010)}

Obviusly, because the numbers are symmetrically distributed around 3939, the mean will be 3939.

And this is the case where we have the smallest largest value in the set, as the numbers are all clustered, for example, if one of the numbers in the lower side was 2 units smaller, then the largest number should be 2 units larger.

Then, the minimum possible value of the largest number is:

3939 + 1010 = 4049