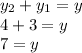Question

Step by step explanation of finding the value of x and y

Answer 1

`x=4√(2)\\y=7`

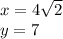
Explanation:

In order to solve this problem, the easiest approach is to draw a line connecting the vertex between the side with a measure of (y) and (3) to the side with the length (x). This side should be parallel to the side with a length of (4).

Since the new side constructed (call this side (b)), is parallel to the side with a length of (4) and is intersected by segments that are perpendicular to the side with a length of (4), the side (b) and (4) must have the same measure. Therefore (b = 4).

The triangle formed with sides (x) and (b) is a (45 - 45 - 90) triangle. Meaning that its angles have the following measure, (45 - 45- 90). This means that its sides follow the following ratio:

angle : side opposite

`45:x\\45:x\\90:x√(2)`

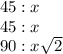
Apply this logic to the given situation.

`x=b*√(2)\\x = 4√(2)`

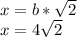
The side (b) divides the side (y) into two parts. Call the part that is a side of the triangle (
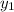`y_1`) the side that is a part of the rectangle is called (
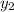`y_2`). As per the logic used to find the lengths of side (b), one can use similar logic to find the length of side (
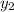`y_2`). The sides (
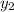`y_2`) and (3) are parallel and are intersected by the sides with a measure of (4) and (b), therefore (
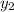`y_2`) and (3) are cognrunet. Thus (
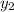`y_2` = 3).

The base angles converse theorem states that when two angles in a triangle are congruent, the triangle is isosceles, and the sides opposite the congruent angles are also congruent. Thus, one can state the following:

`y_1=b\\y_1=4`

Now add up the measurement of (
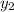`y_2`) and (
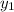`y_1`) to find the measure of (y):

`y_2+y_1=y\\4+3=y\\7=y`