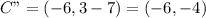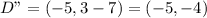Question

Building 1 (Circle) : Rotate 270 degrees counterclockwise around the origin. Building 2 (Square): Reflect across the y axis. Building 3 (Triangle): Reflect across the y axis, then translate 3 up and 2 to the left. Building 4 (L-Shape) : The points A (3, 8), B (6, 8), C (6, 3), and D (5, 3) need to be transformed to points A'' (–3, 1), B'' (–6, 1), C'' (–6, –4), and D'' (–5, –4). Avoid the pond, which is an oval with an origin at (0, 0), a width of 4 units, and a height of 2 units.

Answer 1

See explanation

Explanation:

The question is incomplete, as some coordinates to transform are not given.

I will, however, give a general explanation.

Rotate circle 270 degrees counterclockwise

This implies that, we rotate the center of the circle and the rule of this rotation is:

`(x,y) \to (y,-x)`

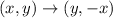
Assume the center is: (5,3), the new center will be: (3,-5)

Reflect square across y-axis

The rule is:

`(x,y) \to (-x,y)`

If the square has (3,5) as one of its vertices before rotation, the new point will be (-3,5).

Reflect triangle across y-axis, then 3 units up and 2 units left

The rule of reflection is:

`(x,y) \to (-x,y)`

If the triangle has (3,5) as one of its vertices before rotation, the new point will be (-3,5).

The rule of translating a point up is:

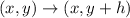`(x,y) \to (x,y+h)` where h is the unit of translation

In this case, h = 3; So, we have:

`(-3,5) \to (-3,5+3)`

`(-3,5) \to (-3,8)`

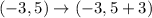
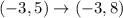
The rule of translating a point left is:

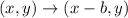`(x,y) \to (x-b,y)` where b is the unit of translation

In this case, b = 2; So, we have:

`(-3,8) \to (-3+2,8)`

`(-3,8) \to (-1,8)`

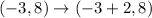
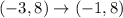
The L shape

`A = (3, 8)`
`A`

`B = (6, 8)`
`B`

`C = (6, 3)`
`C`

`D = (5, 3)`
`D`

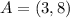
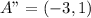
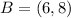
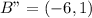
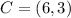
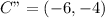
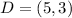
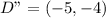
Required

The transformation from ABCD to A"B"C"D"

First, ABCD is reflected across the y-axis.

The rule is:

`(x,y) \to (-x,y)`

So, we have:

`A' = (-3,8)`

`B' = (-6,8)`

`C' = (-6,3)`

`D' = (-5,3)`

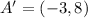
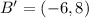
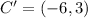
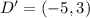
Next A'B'C'D' is translated 7 units down

The rule is:

`(x,y) \to (x,y-7)`

So, we have:

`A`

`B`

`C`

`D`