Answer:
Option (3)
Explanation:
Given function is,
f(x) = 3x² - 2x
=
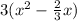
=
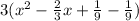
=
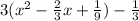
=

Vertex of the parabola →
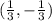
Here, leading coefficient is positive (+3),
Therefore, parabola will open upwards.
In a parabola opening upwards function decreases from negative infinity to the x value of the vertex.
Function will decrease in the interval (-∞,
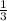 ).
).
Option (3) will be the answer.