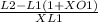Answer:
1. L1 =
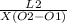
2. O2 =
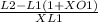
Explanation:
Given: x =
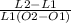
1. To make L1 the subject of formula;
x =
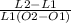
cross multiply to have;
L2 - L1 = xL1(O2 - O1)
collect like terms,
L2 = xL1(O2 - O1) + L1
factorize the right hand side;
L2 = L1[x(O2 - O1)]
L1 =
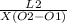
2. To make O2 the subject of formula;
x =
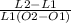
cross multiply to have;
L2 - L1 = xL1(O2 - O1)
open the bracket to have;
L2 - L1 = xL1O2 - xL1O1
⇒ xL1O2 = L2 - L1 + xL1O1
O2 =
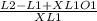
=