Question

The triangles are similar. solve for x

Answer 1

x= 6.25

Explanation:

The hypotenuse of triangle JKL is taken as 96, in the similar way the hypotenuse of triangle JTU is 36. So x can be found by first finding the value of JU, using the Pythagoras theorem.

`a^(2) = b^(2) + c^(2)`

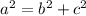
In this shape the formula will be:

`TU^(2) = JT^(2) + JU^(2)`

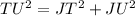
Substitute the given values in the shape into the formula.

TU = 34

JT = 27

TU = Lets take 'y'

`34^(2) = 27^(2) + y^(2)`

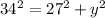
1156 = 729 +
`y^(2)`

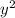
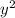`y^(2)` = 1156 - 729

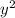`y^(2)` = 427

y =
`√(427)` = 20.7 ( rounded to 1 decimal place) = 21 (rounded to whole number).

So the original value of JU is '21', but we have to find the value of 'x'. So the expression '-4 + 4x' is equal to 21. This can be written as:

-4 + 4x = 21

4x = 21 + 4

4x = 25

∴ x =
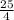`(25)/(4)` = 6.25

x= 6.25