Question

Kenji simplifies 3^5 x 4^ 5and gets the result 12^10, but Darlene is not sure. Is Kenji correct? Justify your answer.

Answer 1

That's a question about exponentiation.

Answer:

Kenji is wrong because he does not aply the porperty correctly.

Explanation:

A exponetiation has this form:

`\boxed{a^b}`

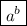
a is the base

b is the power or exponent

To understand that situation it's important to know a property about exponentiation. When we have a multiplication with the same exponent and diferent bases, the result is the multiplication of the bases with the same exponent. Let's see this above, in mathematical language:

`\boxed{a^b \cdot c^b = (a\cdot c) ^b}`

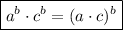
Examples:

• 
  `2^3 \cdot 8^3 = (2 \cdot 8) ^3 = 16^3`

• 
  `10^9 \cdot 23^9 = (10 \cdot 23) ^9 = 230^9`

Now, we can say why Kenji is wrong. It's easy simplify
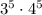`3^5 \cdot 4^5`! We know that the result is
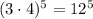`(3 \cdot 4) ^5 = 12^5`, but Kenji multiplied the bases and added the exponents, that's why he is wrong.

I hope I've helped. ^^

Enjoy your studies! \o/