The area of the figure, consisting of a rectangle with a semicircle removed, is approximately
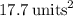 , rounded to the nearest tenth.
, rounded to the nearest tenth.
To find the area of the figure composed of a rectangle with a semicircle removed, follow these steps:
1. Rectangle Area
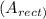 :
:
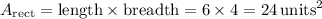
2. Semicircle Area (
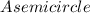 ): The diameter of the semicircle is equal to the breadth of the rectangle (d = 4), and the radius (r) is half of the diameter (r = 2). The formula for the area of a semicircle is
): The diameter of the semicircle is equal to the breadth of the rectangle (d = 4), and the radius (r) is half of the diameter (r = 2). The formula for the area of a semicircle is
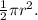
![\[ A_{\text{semicircle}} = (1)/(2) * \pi * (2)^2 = 2 \pi \, \text{units}^2 \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/d8pt18jei75fwu33ae5wmwi15zhfublh5q.png)
3. Area of the Figure (
 ): Subtract the semicircle area from the rectangle area.
): Subtract the semicircle area from the rectangle area.
![\[ A_{\text{total}} = A_{\text{rect}} - A_{\text{semicircle}} = 24 - 2 \pi \approx 17.7 \, \text{units}^2 \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/yi0w0uz836faqzq8z0ct1jt5kbw3ubmqgt.png)