Answer:

Step-by-step explanation:
The pressure on the gas changes, while the temperature remains constant, and we want to find the new volume. So, we will use Boyle's Law, which states there is an inverse relationship between the pressure on a gas and the volume of the gas. The formula is:

The pressure of the gas is originally 985 mm Hg and the volume is 205 milliliters.
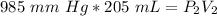
The pressure is decreased to 615 mm Hg, but the new volume is unknown.
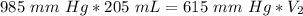
We are solving for the new volume, so we must isolate the variable V₂. It is being multiplied by 615 millimeters of mercury.. The inverse of multiplication is division, so we divide both sides of the equation by 615 mm Hg.
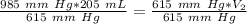

The units of millimeters of mercury (mm Hg) cancel.
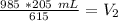
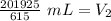
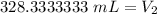
The original measurements have 3 significant figures, so our answer must have the same. For the number we calculated, that is the ones place.
The 3 to the right in the tenths place tells us to leave the 8 in the ones place.
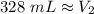
The new volume of the gas is approximately 328 milliliters.