Question

An electron travelling at 7.72 x 107 m/s [E] enters a force field that reduces its velocity to 2.46 x 107 m/s [E]. The acceleration is constant. The displacement during the acceleration is 0.478 m [E]. Determine (a) the electron’s acceleration (b) the time interval over which the acceleration occurs.

Answer 1

Acceleration of this electron:
`-5.60 * 10^(15)\; \rm m \cdot s^(-2)`.

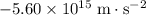Time taken: approximately
`9.39 * 10^(-9)\; \rm s`.

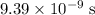Step-by-step explanation:

• Let
  `u` denote the velocity of this electron before the change.
• Let
  `v` denote the velocity of this electron after the change.
• Let
  `x` denote the displacement.
• Let
  `a` denote the acceleration.
• Let
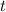  `t` denote the time taken.

Apply the SUVAT equation that does not involve time:

`v^(2) - u^(2) = 2\, a \, x`.

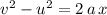Equivalently:

`\begin{aligned}a &= (v^(2) - u^(2))/(2\, x)\end{aligned}`.

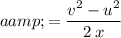By this equation, the acceleration of this electron would be:

`\begin{aligned}a &= (v^(2) - u^(2))/(2\, x) \\ &= ((7.72 * 10^(7)\; \rm m \cdot s^(-1))^(2) - (2.46 * 10^(7) \; \rm m \cdot s^(-1))^(2))/(2 * 0.478\; \rm m) \\ &\approx -5.60 * 10^(15)\; \rm m \cdot s^(-2)\end{aligned}`.

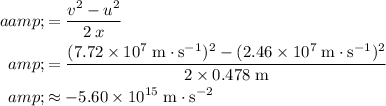The speed of this electron has changed from
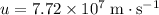`u = 7.72 * 10^(7)\; \rm m\cdot s^(-1)` to
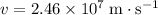`v = 2.46 * 10^(7)\; \rm m \cdot s^(-1)`. Calculate the time required to achieve this change at a rate of
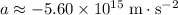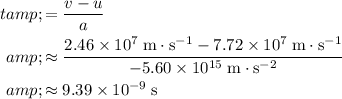`a \approx -5.60 * 10^(15)\; \rm m\cdot s^(-2)`:

`\begin{aligned}t &= (v - u)/(a) \\ &\approx (2.46* 10^(7)\; \rm m \cdot s^(-1) - 7.72 * 10^(7)\; \rm m\cdot s^(-1))/(-5.60 * 10^(15)\; \rm m\cdot s^(-2)) \\ &\approx 9.39 * 10^(-9)\; \rm s\end{aligned}`.