Question

Thank you so much, my friend

Answer 1

Explanation:

This is quite a doozy, my friend. We will set up a d = rt table, fill it in...and pray.

The table will look like this before we even fill anything in:

d = r * t

SUV

sedan

Ok now we start to pick apart the problem. Motion problems are the hardest of all story problems ever. This is because there are about 100 ways a motion problem can be presented. So far what we KNOW for an indisputable fact is that the distance from Georgetown to Greenville is 120 km. So we fill that in, making the table:

d = r * t

SUV 120

sedan 120

The next part is derived from the sentence "After an hour, the SUV was 24 km ahead of the sedan." This tells us the rate of the SUV in terms of the sedan. If the SUV is 24 km ahead of the sedan in 1 hour, that tells us that the rate of the sedan is r and the rate of the SUV is r + 24 km/hr. BUT we have other times in this problem, one of them being 25 minutes. We have a problem here because the times either have to be in hours or minutes, but not both. So we will change that rate to km/min. Doing that:

24
`(km)/(hr)` ×
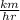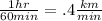`(1hr)/(60min)=.4(km)/(min)` So now we can fill in the rates in the table:

d = r * t

SUV 120 = r + .4

sedan 120 = r

They left at the same time, so now the table looks like this:

d = r * t

SUV 120 = r + .4 * t

sedan 120 = r * t

We will put in the time difference of 25 minutes in just a sec.

If d = rt, then the equation for each row is as follows:

SUV: 120 = (r + .4)t

sedan: 120 = rt

Since the times are the same (because they left at the same time, we will set the equations each equal to t. The distances are the same, too, I know that, but if we set the distances equal to each other and then solve the equations for a variable, the distances cancel each other out, leaving us with nowhere to go. Trust me, I tried that first! Didn't work.

Solving the first equation for time:

sedan:
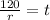`(120)/(r)=t` That's the easy one. Now the SUV. This is where that time difference of 25 minutes comes in from the last sentence. Let's think about what that sentence means in terms of the times of each of these vehicles. If the sedan arrived 25 minutes after the SUV, then the sedan was driving 25 minutes longer; conversely, if the sedan arrived 25 minutes after the SUV, then the SUV was driving 25 minutes less than the sedan. The latter explanation is the one I used in the equation. Again, if the SUV was driving 25 minutes less than the sedan, and the equations are solved for time, then the equation for the SUV in terms of time is

`(120)/(r+.4)=t-25` and we solve that for t:

`(120)/(r+.4)+25=t`

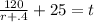
Again, going off the fact that times they both leave are the same, we set the equations equal to one another and solve for r:

`(120)/(r+.4)+25=(120)/(r)`

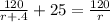
I began by first multiplying everything through by (r + .4) to get rid of it in the denominator. Doing that:

`[r+.4]((120)/(r+.4)) +[r+.4](25)=[r+.4]((120)/(r))` which simplifies very nicely to

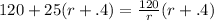`120+25(r+.4)=(120)/(r)(r+.4)` So maybe it's not so nice. Let's keep going:

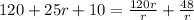`120+25r+10=(120r)/(r)+(48)/(r)` and keep going some more:

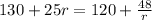`130+25r=120+(48)/(r)` and now we multiply everything through by r to get rid of THAT denominator:

`r(130)+r(25r)=r(120)+r((48)/(r))` giving us:

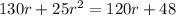`130r+25r^2=120r+48` Now we have a second degree polynomial we have to solve by factoring. Get everything on one side and factor using the quadratic formula.

`25r^2+10r-48=0`

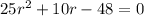
That factors to

r = 1.2 and r = -1.6 and both of those rates are in km/minute. First of all, we cannot have a negative rate (this is not physics where we are dealing with velocity which CAN be negative) so we throw out the -1.6 and convert the rate of 1.2 km/minute back to km/hr:

`1.2(km)/(min)` ×
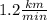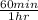`(60min)/(1hr)` and we get

r = 72 km/h, choice B.

Wow...what a pain THAT was, right?!