Question

Distributions and Comparing Data Project

Round all answers to the nearest tenth. Present your work in a neat, legible way. Show all work.
Given the data set (16 values):
8, 6, 10, 5, 7, 1, 6, 11, 5, 13, 14, 8, 11, 9, 8, 6
1. Create a histogram and a box plot to represent this data set. What is the shape of the data
representation? Explain your reasoning.
2. Which measure of center and spread would you use to represent this data? Explain your reasoning.
3. Use a random number generator to generate a set of 15 numbers between 1 and 20. Create a
histogram and box plot to represent your data set. Calculate measures of center and spread. Which
measure of center and spread would you use to represent your data?
For questions 6-9 refer to the box plots (Assume their positions are on same number line). Write your
Class A
Class B
Class C
Class D
o
4. Which class(es) appear to have the most consistent scores? Explain your reasoning,

Answer 1

1. The shape of the histogram created with MS Excel is approximately bell shaped and approximately evenly spread about the central (largest counts) values

The shape of the box plot created with MS Excel is approximately evenly distributed

2. The appropriate measure of central tendency for a bell shaped histogram is the mean and median, due to the approximately equal distribution about the highest frequency class

3. Part A

The 15 numbers between 1 and 20 generated by a random generator are;

1, 8, 8, 15, 4, 18, 11, 6, 17, 1, 18, 15, 10, 12, 11

The measure of center is the mean = (1+8+8+15+4+18+11+6+17+1+18+15+10+12+11)/15 = 155/15 = 31/3

The measure of spread used is the variance, s² = 32.38

`Where, \,s^2 =(\sum \left (x_i-\bar x \right )^(2) )/(n - 1)`

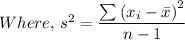
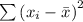`{\sum \left (x_i-\bar x \right )^(2) }` = 453.333

n = 15

s² = 453.
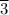`\overline 3`/(15 - 1) = 32.38

Part B

The measure of central tendency are the mean and the median because the size of the data (n = 15), is 75% of the population (N = 20) nd therefore the data is approximately normal and can be represented by the mean and the standard deviation

Explanation: