Question

A BYU-Idaho professor took a survey of his classes and found that 82 out of 90 people who had served a mission had personally met a member of the quorum of the twelve apostles. Of the non-returned missionaries that were surveyed 86 of 110 had personally met a member of the quorum of the twelve apostles. Calculate a 99% confidence interval for the difference in the two proportions.

Answer 1

The 99% confidence interval for the difference in the two proportions is (-0.0247, 0.2833).

Explanation:

Before building the confidence interval, we need to understand the Central Limit Theorem and subtraction of normal variables.

Central Limit Theorem

The Central Limit Theorem establishes that, for a normally distributed random variable X, with mean
`\mu` and standard deviation
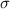`\sigma`, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
`\mu` and standard deviation
`s = (\sigma)/(√(n))`.

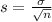For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean
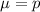`\mu = p` and standard deviation
`s = \sqrt{(p(1-p))/(n)}`

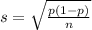
A BYU-Idaho professor took a survey of his classes and found that 82 out of 90 people who had served a mission had personally met a member of the quorum of the twelve apostles.

This means that:

`p_S = (82)/(90) = 0.9111`

`s_S = \sqrt{(0.9111*0.0888)/(90)} = 0.045`

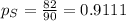
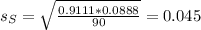
Of the non-returned missionaries that were surveyed 86 of 110 had personally met a member of the quorum of the twelve apostles.

This means that:

`p_N = (86)/(110) = 0.7818`

`s_N = \sqrt{(0.7818*0.2182)/(110)} = 0.0394`

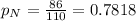
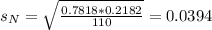
Distribution of the difference:

`p = p_S - p_N = 0.9111 - 0.7818 = 0.1293`

`s = √(s_S^2+s_N^2) = √(0.045^2+0.0394^2) = 0.0598`

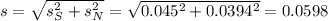
Calculate a 99% confidence interval for the difference in the two proportions.

The confidence interval is:

`p \pm zs`

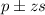
In which

z is the z-score that has a p-value of
`1 - (\alpha)/(2)`.

99% confidence level

So
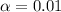`\alpha = 0.01`, z is the value of Z that has a p-value of
`1 - (0.01)/(2) = 0.995`, so
`Z = 2.575`.

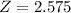The lower bound of the interval is:

`p - zs = 0.1293 - 2.575*0.0598 = -0.0247`

`p + zs = 0.1293 + 2.575*0.0598 = 0.2833`

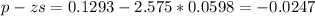
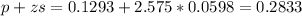
The 99% confidence interval for the difference in the two proportions is (-0.0247, 0.2833).