Question

Use the​ Gauss-Jordan method to solve the system of equations. If the system has infinitely many​ solutions, give the solution with z arbitrary

Answer 1

Write each equation in standard form:

3x + y + 3z = 11

x + 2y + z = 7

-x + y + z = 0

In matrix form, this is

`\begin{bmatrix}3&1&3\\1&2&1\\-1&1&1\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}11\\7\\0\end{bmatrix}`

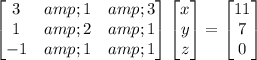
and in augmented matrix form,

`\left[\begin{array}ccc3&1&3&11\\1&2&1&7\\-1&1&1&0\end{bmatrix}\right]`

Now for the row operations:

• Add row 1 to -3 (row 2), and add row 1 to 3 (row 3):

`\left[\begin{array}c3&1&3&11\\0&-5&0&-10\\0&4&6&11\end{bmatrix}\right]`

• Multiply row 2 by -1/5:

`\left[\begin{array}c3&1&3&11\\0&1&0&2\\0&4&6&11\end{bmatrix}\right]`

• Add -4 (row 2) to row 3:

`\left[\begin{array}c3&1&3&11\\0&1&0&2\\0&0&6&3\end{bmatrix}\right]`

• Multiply row 3 by 1/6:

`\left[\begin{array}c3&1&3&11\\0&1&0&2\\0&0&1&\frac12\end{bmatrix}\right]`

• Add -1 (row 2) and -3 (row 3) to row 1:

`\left[\begin{array}ccc3&0&0&\frac{15}2\\0&1&0&2\\0&0&1&\frac12\end{bmatrix}\right]`

• Mutiply row 1 by 1/3:

`\left[\begin{array}ccc1&0&0&\frac52\\0&1&0&2\\0&0&1&\frac12\end{bmatrix}\right]`

Then the solution to the system is (x, y, z) = (5/2, 2, 1/2).