Answer:
The null hypothesis is

The alternative hypothesis is

The p-value of the test is 0.1148 > 0.05, which means that the sample does not give enough evidence to conclude that the machine is underfilling the bags.
Explanation:
A manufacturer of potato chips would like to know whether its bag filling machine works correctly at the 444 gram setting.
At the null hypothesis, we test if the machine works correctly, that is, the mean is of 444. So

At the alternative hypothesis, we test if they are underfilling, that is, if the mean is of less than 444. So

The test statistic is:
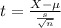
In which X is the sample mean,
 is the value tested at the null hypothesis, s is the standard deviation and n is the size of the sample.
is the value tested at the null hypothesis, s is the standard deviation and n is the size of the sample.
444 is tested at the null hypothesis:
This means that
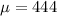
A 41 bag sample had a mean of 440 grams with a variance of 441.
This means that

Value of the test statistic:
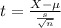
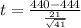
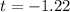
P-value of the test:
Right-tailed test(test if the mean is less than a value), with 41 - 1 = 40 df and t = -1.22.
Using a t-distribution calculator, this p-value is of 0.1148
The p-value of the test is 0.1148 > 0.05, which means that the sample does not give enough evidence to conclude that the machine is underfilling the bags.