Question

The weights of certain machine components are normally distributed with a mean of 5.19 ounces and a standard deviation of 0.05 ounces. Find the two weights that separate the top 8% and the bottom 8%. These weights could serve as limits used to identify which components should be rejected

Answer 1

The weight that separate the top 8% by 5.2605 and the weight that separate bottom 8% by 5.1195.

Explanation:

We are given that

Mean,
`\mu=5.19`

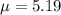
Standard deviation,
`\sigma=0.05`

We have to find the two weights that separate the top 8% and the bottom 8%.

Let x1 and x2 the two weights that separate the top 8% and the bottom 8%.

Z-value for p-value =0.08 =
`-1.41`

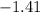
For 8% bottom

`Z=(x_1-\mu)/(\sigma)=-1.41`

`(x_1-5.19)/(0.05)=-1.41`

`x_1-5.19=-1.41* 0.05`

`x_1=-1.41* 0.05+5.19`

`x_1=5.1195`

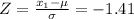
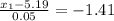
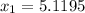
For 8% top

p-Value=1-0.08=0.92

Z- value=1.41

Now,

`(x_2-5.19)/(0.05)=1.41`

`x_2-5.19=1.41* 0.05`

`x_2=1.41* 0.05+5.19`

`x_2=5.2605`

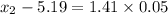
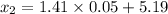
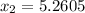
(x1,x2)=(5.1195,5.2605)