Question

1. A manufacturing cell with two workers is responsible for producing a small frying pan with a required takt time of 496 seconds. The material passes through two processes: a deep drawing process and a trimming process. The average cycle time for the deep drawing process is 450 seconds and average cycle time for trimming is 430 seconds. (2 pts.)

a. Does the work cell have adequate capacity to meet demand? Explain.
b. What is the required daily production capacity of the work cell (in number of frying pans per day)? Assume 480 minutes/workday of available time.
2. What is the total daily idle time for both workers in Problem 1? Report your answer in (a) seconds of idle time and (b) as a percentage of total working time for the cell. (2 pts.)

Answer 1

Step-by-step explanation:

`496=(480* 60)/(demand)`

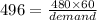
demand per day = 58 pans

Due to availability of two workers we can have parallel we can have deep drawing and trimming operations simultaneously.

Hence the cycle time would be the greater time of the two operations.

cycle time = 450 seconds

`\text{capacity of work cell}=\frac{\text{available working time}}{\text{cycle time}}`

`\text{capacity of work cell}=(480* 60)/(450)`

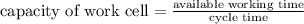
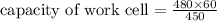
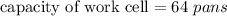`\text{capacity of work cell}=64 ~pans` (which is greater than the demand of 58 pans)

Therefore the work cell has sufficient capacity and time (496 sec.>cycle time 450 sec) to meet the demand.

b)

Required daily production is 58 pans