Question

Children arrive at a house to do Halloween trick-or- treating according to a Poisson process at the unlucky rate of 13/hour. What is the probability that the time between the 15th and 16th arrivals will be more than 4 minutes ? (Hint: Think exponential.)

a) e e-2 = 0.1353
b) e-13/15 = 0.4204
c) e-1 = 0.3679
d) 1-2-1 = 0.6321

Answer 1

0.4204 probability, option b.

Explanation:

Exponential distribution:

The exponential probability distribution, with mean m, is described by the following equation:

`f(x) = \mu e^(-\mu x)`

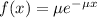
In which
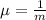`\mu = (1)/(m)` is the decay parameter.

The probability that x is lower or equal to a is given by:

`P(X \leq x) = \int\limits^a_0 {f(x)} \, dx`

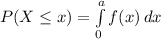
Which has the following solution:

`P(X \leq x) = 1 - e^(-\mu x)`

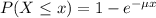
The probability of finding a value higher than x is:

`P(X > x) = 1 - P(X \leq x) = 1 - (1 - e^(-\mu x)) = e^(-\mu x)`

Children arrive at a house to do Halloween trick-or- treating according to a Poisson process at the unlucky rate of 13/hour

13 arrivals during an hour, which means that the mean time between arrivals, in minutes is of
`\mu = (13)/(60) = 0.2167`

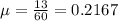
What is the probability that the time between the 15th and 16th arrivals will be more than 4 minutes ?

This is P(X > 4). So

`P(X > 4) = e^(-0.2167*4) = 0.4204`

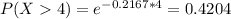
So the correct answer is given by option b.