Question

(4 + 4i)/(5+4i) = divide

Answer 1

B.

Explanation:

`(4 + 4i)/(5 + 4i)`

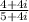
• Multiplying both numerator and denominator by (5 - 4i) , the conjugate of the denominator, i. e, (5 + 4i).

`(4 + 4i)/(5 + 4i) * (5 - 4i)/(5-4i)`

`((4 + 4i)(5 - 4i))/((5 + 4i)(5 - 4i))`

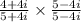
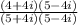
• Multiplying (4+4i) and (5-4i) using distributive property
• Using the identity (a+b)(a-b)= a² - b² where 5 will act as a and 4i will act as b

`\frac{20-16i+20i-16i^2}{(5) {}^(2) - (4i) {}^(2) }`

• i² = -1

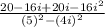
(combining like terms)

`(20+(-16i+20i)-(-16))/(25-(-16))`

`((20+16)+4i)/(25+16)`

`(36+4i)/(41)`

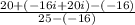
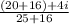
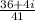
distributing the denominator

`(36)/(41) + (4)/(41)i`

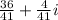
That is, option B.