Question

Someone help me please

Answer 1

9514 1404 393

Answer:

• A = (0, 1)
• B = (3, -2)
• area = 4.5 square units

Explanation:

Rewriting the equations to make x the subject, we have ...

x = y² -1 . . . . . [eq1]

x = 1 - y . . . . . .[eq2]

At the points of intersection, the difference will be zero.

y² -1 -(1 -y) = 0

y² +y -2 = 0

(y -1)(y +2) = 0

The y-coordinates of points A and B are 1 and -2.

The corresponding x-coordinates are ...

x = 1 -{1, -2} = {1 -1, 1+2} = {0, 3}

Then A = (0, 1) and B = (3, -2).

__

A differential of area can be written ...

(x2 -x1)dy = ((1 -y) -(y² -1))dy = (2 -y -y²)dy

Integrating this over the interval y = [-2, 1] gives the area.

`\displaystyle A=\int_(-2)^1(2-y-y^2)\,dy=\left.(2y-(1)/(2)y^2-(1)/(3)y^3)\right|_(-2)^1\\\\=\left(2-(1)/(2)-(1)/(3)\right)-\left(2(-2)-((-2)^2)/(2)-((-2)^3)/(3)\right)=(7)/(6)+4+2-(8)/(3)\\\\=\boxed{4.5}`

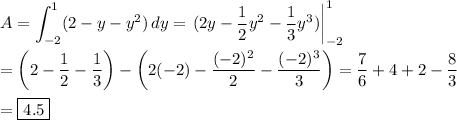
The area of the shaded region is 4.5 square units.