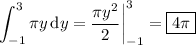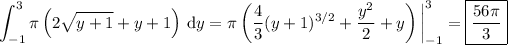Question

The shaded region R in diagram below is enclosed by y-axis, y = x^2 - 1 and y = 3.

Determine the volume of the solid generated when the shaded region R is revolved
about x = -1 by using Disk method.

Answer 1

Cross sections of the volume are washers or annuli with outer radii x(y) + 1, where

y = x(y) ² - 1 ==> x(y) = √(y + 1)

and inner radii 1. The distance between the outermost edge of each shell to the axis of revolution is then 1 + √(y + 1), and the distance between the innermost edge of R on the y-axis to the axis of revolution is 1.

For each value of y in the interval [-1, 3], the corresponding cross section has an area of

π (1 + √(y + 1))² - π (1)² = π (2√(y + 1) + y + 1)

Then the volume of the solid is the integral of this area over [-1, 3]:

`\displaystyle\int_(-1)^3\pi y\,\mathrm dy = \frac{\pi y^2}2\bigg|_(-1)^3 = \boxed{4\pi}`

`\displaystyle\int_(-1)^3 \pi\left(2√(y+1)+y+1\right)\,\mathrm dy = \pi\left(\frac43(y+1)^(3/2)+\frac{y^2}2+y\right)\bigg|_(-1)^3 = \boxed{\frac{56\pi}3}`