Question

cone is inscribed in a cylinder. A square pyramid is inscribed in a rectangular prism. The cone and the pyramid have the same volume. Part of the volume of the cylinder, 1 V 1 , is not taken up by the cone. Part of the volume of the rectangular prism, 2 V 2 , is not taken up by the square pyramid. What is the relationship of these two volumes, 1 V 1 and 2 V 2 ?

Answer 1

The answer is "
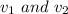`v_1 \ and\ v_2` are equal".

Explanation:

Its volume could be defined both by cone as well as the cylinders

`\to \text{(base area)} * \text{(solid height)} * ((1)/(3))\\\\`

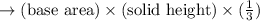
We are planning to write this as
`V = (Bh)/(3)`

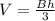
When we relate this formula to the cylindrical and prism volume formula, we can see that when we multiply the cone volume by 3, the cylinder size where it is registered comes in. The very same goes for the pyramid as well as the inscription of the rectangular prism. That both pyramid and the cone have the same volume V, hence it would have the same volume of a cell and rectangle prism.
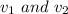`v_1 \ and\ v_2` are so similar.