Question

A magnetic field of 0.080 T is in the y-direction. The velocity of wire segment S has a magnitude of 78 m/s and components of 18 m/s in the x-direction, 24 m/s in the y-direction, and 72 m/s in the z-direction. The segment has length 0.50 m and is parallel to the z-axis as it moves.

Required:
a. Find the motional emf induced between the ends of the segment.
b. What would the motional emf be if the wire segment was parallel to the y-axis?

Answer 1

Step-by-step explanation:

From the information given:

The motional emf can be computed by using the formula:

`E = L^(\to)*(V^\to*\beta^(\to))`

`E = L^(\to)*((x+y+z)*\beta^(\to))`

`E = 0.50*((18\hat i+24 \hat j +72 \hat k )*0.0800)`

`E = 0.50*((18*0.800)\hat k +0j+(72*0.080) \hat -i ))`

`E = 0.50*((18*0.800)`

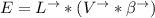
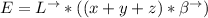
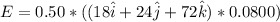
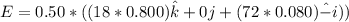
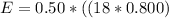
E = 0.72 volts

According to the question, suppose the wire segment was parallel, there will no be any emf induced since the magnetic field is present along the y-axis.

As such, for any motional emf should be induced, the magnetic field, length, and velocity are required to be perpendicular to one another .

Then the motional emf will be:

`E = 0.50 \hat j *((18*0.800)\hat k -(72*0.080) \hat i ))`

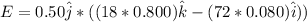
E = 0 (zero)