Question

Date
Prove that sintheta sec theta+costheta cosec theta=
2 cosec 2theta​

Answer 1

See Below.

Explanation:

We want to prove that:

`\displaystyle \sin\theta\sec\theta+\cos\theta\csc\theta = 2\csc2\theta`

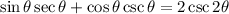
Let secθ = 1 / cosθ and cscθ = 1 / sinθ:

`\displaystyle (\sin\theta)/(\cos\theta)+(\cos\theta)/(\sin\theta)=2\csc2\theta`

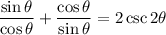
Creat a common denominator. Multiply the first fraction by sinθ and the second by cosθ. Hence:

`\displaystyle (\sin^2\theta)/(\sin\theta\cos\theta)+(\cos^2\theta)/(\sin\theta\cos\theta)=2\csc2\theta`

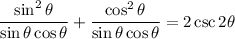
Combine fractions:

`\displaystyle (\sin^2\theta + \cos^2\theta)/(\sin\theta\cos\theta)=2\csc2\theta`

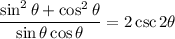
Simplify. Recall that sin²θ + cos²θ = 1:

`\displaystyle (1)/(\sin\theta\cos\theta)=2\csc2\theta`

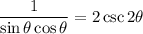
Multiply the fraction by two:

`\displaystyle (2)/(2\sin\theta\cos\theta)=2\csc2\theta`

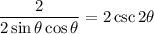
Recall that sin2θ = 2sinθcosθ. Hence:

`\displaystyle (2)/(\sin2\theta)=2\csc2\theta`

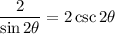
By definition:

`\displaystyle 2\csc2\theta = 2\csc2\theta`

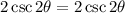
Hence proven.