Question

Solve the exponential equation by taking the logarithm on both sides. 5^(x+8)=7

Answer 1

x = (log₅7) - 8

Step-by-step explanation:

Given;

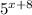`5^(x+8)` = 7

Take log of both sides;

log₁₀(
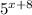`5^(x+8)`) = log₁₀7 -------------(ii)

From the laws of logarithm remember that;

logₐ xⁿ = n logₐ x

Equation (ii) can then be written as;

(x + 8)log₁₀5 = log₁₀7

Divide both sides by log₁₀5

(x + 8) =
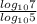`(log_(10)7)/(log_(10)5)` -----------(iii)

From the laws of logarithm, remember that;

`(log_(a)x)/(log_(a)y) = log_yx`

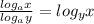
Equation (iii) can thus be written as;

(x + 8) = log₅7

x + 8 = log₅7

Make x subject of the formula;

x = (log₅7) - 8