Question

A town recently dismissed 5 employees in order to meet their new budget reductions. The town had 4 employees over 50 years of age and 16 under 50. If the dismissed employees were selected at random, what is the probability that no more than 1 employee was over 50

Answer 1

0.7513 = 75.13% probability that no more than 1 employee was over 50

Explanation:

The employees are chosen from the sample without replacement, which means that the hypergeometric distribution is used to solve this question.

Hypergeometric distribution:

The probability of x successes is given by the following formula:

`P(X = x) = h(x,N,n,k) = (C_(k,x)*C_(N-k,n-x))/(C_(N,n))`

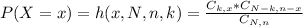
In which:

x is the number of successes.

N is the size of the population.

n is the size of the sample.

k is the total number of desired outcomes.

Combinations formula:

`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

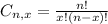
In this question:

4 + 16 = 20 employees, which means that
`N = 20`

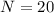
4 over 50, which means that
`k = 4`

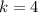
5 were dismissed, which means that
`n = 5`

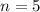
What is the probability that no more than 1 employee was over 50?

Probability of at most one over 50, which is:

`P(X \leq 1) = P(X = 0) + P(X = 1)`

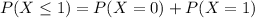
In which

`P(X = x) = h(x,N,n,k) = (C_(k,x)*C_(N-k,n-x))/(C_(N,n))`

`P(X = 0) = h(0,20,5,4) = (C_(4,0)*C_(16,5))/(C_(20,5)) = 0.2817`

`P(X = 1) = h(1,20,5,4) = (C_(4,1)*C_(16,4))/(C_(20,5)) = 0.4696`

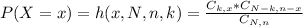
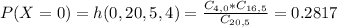
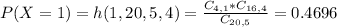
Then

`P(X \leq 1) = P(X = 0) + P(X = 1) = 0.2817 + 0.4696 = 0.7513`

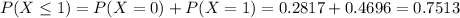
0.7513 = 75.13% probability that no more than 1 employee was over 50