Question

Precision manufacturing: A process manufactures ball bearings with diameters that are normally distributed with mean 25.0 millimeters and standard deviation 0.07 millimeter. Round the answers to at least four decimal places. (a) Find the 60th percentile of the diameters. (b) Find the 67th percentile of the diameters. (c) A hole is to be designed so that 2% of the ball bearings will fit through it. The bearings that fit through the hole will be melted down and remade. What should the diameter of the hole be

Answer 1

a) The 60th percentile of the diameters is of 25.0177 millimeters.

b) The 67th percentile of the diameters is of 25.0308 millimeters.

c) The diameter of the hole should be of 24.8562 millimeters.

Explanation:

Normal Probability Distribution

Problems of normal distributions can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
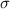`\sigma`, the z-score of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

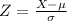
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.

Normally distributed with mean 25.0 millimeters and standard deviation 0.07 millimeter.

This means that
`\mu = 25, \sigma = 0.07`

(a) Find the 60th percentile of the diameters.

This is X when Z has a p-value of 0.6, so X when Z = 0.253.

`Z = (X - \mu)/(\sigma)`

`0.253 = (X - 25)/(0.07)`

`X - 25 = 0.253*0.07`

`X = 25.0177`

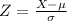
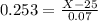
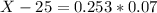
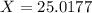
The 60th percentile of the diameters is of 25.0177 millimeters.

(b) Find the 67th percentile of the diameters.

This is X when Z has a p-value of 0.67, so X when Z = 0.44.

`Z = (X - \mu)/(\sigma)`

`0.44 = (X - 25)/(0.07)`

`X - 25 = 0.44*0.07`

`X = 25.0308`

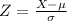
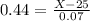
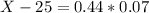
The 67th percentile of the diameters is of 25.0308 millimeters.

(c) A hole is to be designed so that 2% of the ball bearings will fit through it. The bearings that fit through the hole will be melted down and remade. What should the diameter of the hole be.

This is the 2nd percentile, which is X when Z has a p-value of 0.08, so X when Z = -2.054.

`Z = (X - \mu)/(\sigma)`

`-2.054 = (X - 25)/(0.07)`

`X - 25 = -2.054*0.07`

`X = 24.8562`

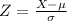
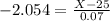
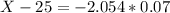
The diameter of the hole should be of 24.8562 millimeters.