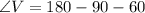Question

Solve the right triangle. 4 3 E F D 60° Write your answers in simplified, rationalized form. Do not round.

Answer 1

`VW = 6`

`WX = 2√(3)`

`\angle V = 30`

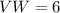
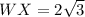
Explanation:

Given

`VX = 4\sqrt{3`

`\angle X = 60^\circ`

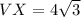
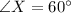
See attachment for right triangle

Required

Solve for VW, WX and
`\angle V`

First, calculate VW

To do this, we make use of:

`sin(\theta) = (Opposite)/(Hypotenuse)`

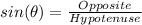
In this case,

`sin(60) = (VW)/(4√(3))`

Make VW the subject

`VW = 4√(3) * sin(60)`

In radical form:

`sin(60) = (√(3))/(2)`

`VW = 4√(3) * (√(3))/(2)`

`VW = (4√(3) * √(3))/(2)`

`VW = (4*3)/(2)`

`VW = (12)/(2)`

`VW = 6`

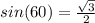
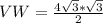
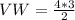
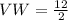
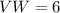
To solve for WX, we make use of Pythagoras Theorem, we make use of:

`VX^2 = VW^2 + WX^2`

`(4√(3))^2 = 6^2 + WX^2`

`16*3 = 36 + WX^2`

`48= 36 + WX^2`

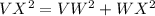
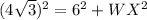
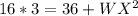
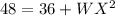
Subtract 36 from both sides

`48 - 36 = 36 - 36 + WX^2`

`48 - 36 = WX^2`

`12= WX^2`

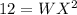
Take the square root of both sides

`√(12)= WX`

`√(4*3)= WX`

`√(4)*√(3)= WX`

`2√(3)= WX`

`WX = 2√(3)`

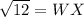
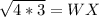
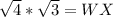
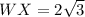
Solving
`\angle V`

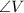
To do this, we make use of:

`\angle V + \angle X + 90 = 180`

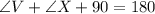
Make V the subject

`\angle V = 180 - 90 - \angle X`

`\angle V = 180 - 90 - 60`

`\angle V = 30`