Question

If $3000 is invested at 3% interest, find the value of the investment at the end of 7 years if the interest is compounded as follows. (Round your answers to the nearest cent.)

(i) annually
(ii) semiannually
(iii) monthly
(iv) weekly
(v) daily
(vi) continuously

Answer 1

annualy=$3689.62

semiannually=$3695.27

monthly=$3700.06

weekly=$3700.81

daily=$3701.00

Continuously=$3701.03

Explanation:

Given:

P=3000

r=3%

t=7 years

Formula used:

Where,

A represents Accumulated amount

P represents (or) invested amount

r represents interest rate

t represents time in years

n represents accumulated or compounded number of times per year

Solution:

(i)annually

n=1 time per year

`A=3000[1+(0.03)/(1) ]^1^(^7^)\\ =3000(1.03)^7\\ =3689.621596\\`

On approximating the values,

A=$3689.62

(ii)semiannually

n=2 times per year

`A=3000[1+(0.03)/(2)^(2(4)) ]\\ =3000[1+0.815]^14\\ =3695.267192`

On approximating the values,

A=$3695.27

(iii)monthly

n=12 times per year

`A=3000[1+(0.03)/(12)^(12(7)) \\ =3000[1+0.0025]^84\\ =3700.0644`

On approximating,

A=$3700.06

(iv) weekly

n=52 times per year

`A=3000[1+(0.03)/(52)]^3^6 \\ =3000(1.23360336)\\ =3700.81003`

On approximating,

A=$3700.81

(v) daily

n=365 time per year

`A=3000[1+(0.03)/(365)]^(365(7)) \\ =3000[1.000082192]^(2555)\\ =3701.002234`

On approximating the values,

A=$3701.00

(vi) Continuously

`A=Pe^r^t\\ =3000e^{(0.03)/(1)(7) }\\ =3000e^(0.21) \\ =3000(1.23367806)\\ =3701.03418\\`

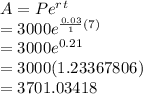
On approximating the value,

A=$3701.03