Answer:
1. 0.2013 = 20.12% probability that exactly 3 will have defective wrapping.
2. 0.1209 = 12.09% probability that at least 4 will have defective wrapping.
3. 0.9671 = 96.71% probability that at most 4 will have defective wrapping.
4. 0.6242 = 62.42% probability that at least 2 will have defective wrapping.
5. 2
6. 1.265
Explanation:
For each product, there are only two possible outcomes. Either it is defective, or it is not. The probability of a product being defective is independent of any other product, which means that the binomial probability distribution is used to solve this question.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.
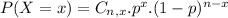
In which
 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.
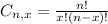
And p is the probability of X happening.
20% of the product wrappings are defective.
This means that
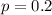
10 products are selected at random
This means that

1. Exactly 3 will have defective wrapping
This is P(X = 3). So
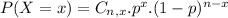
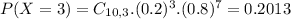
0.2013 = 20.12% probability that exactly 3 will have defective wrapping.
2. At least 4 will have defective wrapping
This is:
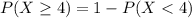
In which:
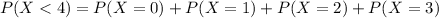
So
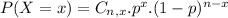
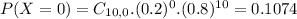
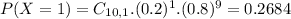
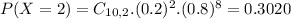
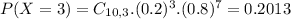
Then
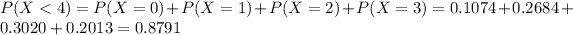
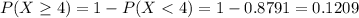
0.1209 = 12.09% probability that at least 4 will have defective wrapping.
3. At most 4 will have defective wrapping

In the previous item, the only missing was P(X = 4). So
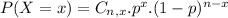
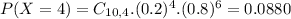
So
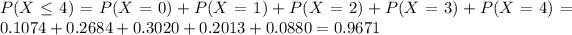
0.9671 = 96.71% probability that at most 4 will have defective wrapping.
4. At least 2 will have defective wrapping
This is:
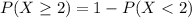
In which

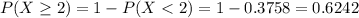
0.6242 = 62.42% probability that at least 2 will have defective wrapping.
5. Calculate the mean (i.e. expected value of x)
For the binomial distribution:

So
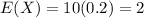
The mean is of 2.
6. Calculate the standard deviation
For the binomial distirbution:
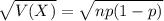
In this case
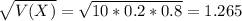
The standard deviation is of 1.265.